音速の計算
空気中の音速は「秒速 340m」と覚えておいても大抵問題ないのだが、空気の温度によって音速は大きく変化する。また風向きとかでも変化してしまう。この 340m/s(秒)は摂氏 15 度のときの速さになる。温度で速度が変わるのは、空気を構成する分子の運動速度が温度が上がるほど速くなるから。
空気は温度以外に、湿度や気圧などの変化もある。音速は気圧の変化には影響を受けないが、音圧は影響を受ける。また湿度にも影響を受けるが、温度変化に比べれば、影響は少ないため通常は考慮しない。
温度が変化すると密度も変化する。密度が変化することで音速が変わるという言い方もできそうだが、なかなか手ごわい話になりそうなので、ここでは触れない。下のプログラムでは、温度から密度を計算している。
まず元となる式はこれで、結構シンプル。
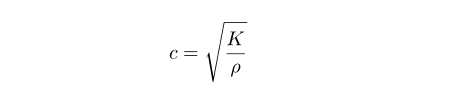
c 音速は通常これを使う 単位は m/s
K 体積弾性率
ρ 密度
体積弾性率を空気の場合に限定してみる。

γ は比熱比
P0 はヘクトパスカル 標準大気圧 1013.25 hPa となるが、単位をそろえるために 101325 Pa(N/m2) これを使う。

γ 比熱比を分解してみる
γ = cp/cv
cp 低圧比熱 1.006
cv 定積比熱 0.717
1.006 / 0.717 = 1.403068340306834

今度は温度によって、密度 ρが変化するので、それに対応させる。温度と気圧から求める。

273.15 は摂氏温度(セルシウス温度)を絶対温度変換するため。
t は摂氏温度
P0 は気圧 101325 Pa(N/m2)
R は気体定数 2.87
これで温度ごとに音速が計算できる。上記をすべてひとつの式に入れるとこうなる。整理していないので、かなり汚い。中身で何を計算しているのか分かりやすいので、下の計算プログラムは、この式をそのまま使っている。

実は式を整理していくと下のように気圧は消えてしまう。音速は気圧に影響を受けないことを物語っている。

また温度以外を固定してしまえば以下の式に落ち着く。普通計算するときはこれで十分。t に摂氏温度を入れて計算する。
c = 331.5 + 0.607t
ちなみに絶対零度の-273.15度を入れて計算してみると音速は0になる。つまり音が存在しない世界。
周波数による音の認識スピードの実験。左チャンネルは440Hzのサイン波、右チャンネルは55Hzのサイン波を4回鳴らしている。高い周波数の440Hzに比べ55Hzは遅れて聴こえるというか、立ち上がりが緩やかに聴こえると思う。

中学生ぐらいから学ぶフーリエ変換 目次はこちら
空気は温度以外に、湿度や気圧などの変化もある。音速は気圧の変化には影響を受けないが、音圧は影響を受ける。また湿度にも影響を受けるが、温度変化に比べれば、影響は少ないため通常は考慮しない。
温度が変化すると密度も変化する。密度が変化することで音速が変わるという言い方もできそうだが、なかなか手ごわい話になりそうなので、ここでは触れない。下のプログラムでは、温度から密度を計算している。
音速の計算
音速は波動方程式から導いているが、細かくやると大変なので、流体中の音速の方程式からスタートして、空気専用にまで式を変形させてみたい。まず元となる式はこれで、結構シンプル。
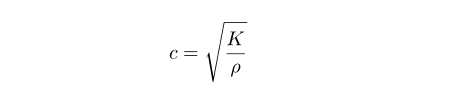
c 音速は通常これを使う 単位は m/s
K 体積弾性率
ρ 密度
体積弾性率を空気の場合に限定してみる。

γ は比熱比
P0 はヘクトパスカル 標準大気圧 1013.25 hPa となるが、単位をそろえるために 101325 Pa(N/m2) これを使う。

γ 比熱比を分解してみる
γ = cp/cv
cp 低圧比熱 1.006
cv 定積比熱 0.717
1.006 / 0.717 = 1.403068340306834

今度は温度によって、密度 ρが変化するので、それに対応させる。温度と気圧から求める。

273.15 は摂氏温度(セルシウス温度)を絶対温度変換するため。
t は摂氏温度
P0 は気圧 101325 Pa(N/m2)
R は気体定数 2.87
これで温度ごとに音速が計算できる。上記をすべてひとつの式に入れるとこうなる。整理していないので、かなり汚い。中身で何を計算しているのか分かりやすいので、下の計算プログラムは、この式をそのまま使っている。

実は式を整理していくと下のように気圧は消えてしまう。音速は気圧に影響を受けないことを物語っている。

また温度以外を固定してしまえば以下の式に落ち着く。普通計算するときはこれで十分。t に摂氏温度を入れて計算する。
c = 331.5 + 0.607t
音速と空気密度の計算プログラム
摂氏温度と気圧を入れることで、空気の密度を出して音速を計算する。気圧は密度計算には影響を及ぼすが、0でなければ音速の結果には影響がない。低圧比熱、定積比熱は通常いじる必要はないと思う。ちなみに絶対零度の-273.15度を入れて計算してみると音速は0になる。つまり音が存在しない世界。
音速と周波数
音楽をやっている人の中では、周波数が高いと音速が速く、低いと遅いと思う人が結構いるらしい。上記のように音速は周波数には依存しないので、高くても低くても同じ速さなのだが、なぜ、こういう誤解が生まれるのか、ちょっと心当たりがあるので書いてみる。結論としては、音程を認識するまでの時間は周波数に依存するからだと思う。例えば人には聴こえないが、1Hzの周波数を認識するには最低でも1秒必要となる。1秒以内に1Hzを認識することは不可能。実際には繰り返し波として聞こえないと、音程としては認識しにくいので、もっと時間は必要だろう。逆に高い音は1秒間に何百、何千と振動を繰り返してくれるので、短い時間で認識できる。特に人が認識しやすい周波数は 2~3kHz ぐらいなので、その周辺の周波数であれば、瞬時に何の音か分かったりする。この差が音楽だと、結構速い遅いの印象になりやすいと思う。音楽では1秒を8分割(テンポ120の時の16分音符)ぐらいにするのは普通なので、ベースの最低音であるE音41Hzなんて音は、この間、5回ぐらいしか振動していない。実際には多分これをちゃんと聞き取ることはできないと思うので、その倍音を人は聞いているのだと思う。基音はほとんど音圧というか振動という印象だと思う。高い音なら 1/8 秒でもしっかり分かるが、低くなると、瞬時には分からないが、しばらくすると音程が判明する。こんなところが音が遅れている印象になってしまうのではないだろうか。周波数による音の認識スピードの実験。左チャンネルは440Hzのサイン波、右チャンネルは55Hzのサイン波を4回鳴らしている。高い周波数の440Hzに比べ55Hzは遅れて聴こえるというか、立ち上がりが緩やかに聴こえると思う。

中学生ぐらいから学ぶフーリエ変換 目次はこちら
