FIR FFT overlap-add method の実験
FIRフィルタを作る場合には必須の手法。サンプル数が長い、もしくは不明な入力信号と、サンプル数が分かっている(少ない)フィルタをFFTで畳み込んでみる。手法は overlap-add method を使う。これは入力信号を一定のサンプル数で切ってから、FFTにかけて変換し、複素数としてフィルタと演算後、iFFTで戻す。戻った細切れの信号はフィルタ分-1長くなるので、その部分をオーバーラップしながら足して、出力信号とするもの。
下図は、この記事のプログラムを図式化したもの。数字はサンプル数でプログラムと対応している。色の付いていないマスにはデータがないので値0を入れている。FilterのFFT処理はレイアウト上、矢印が引けなかったので、唐突に黄色く8サンプルで出てくるけど、上段のFilterの色がある3サンプルに値0の5サンプルを加えて8サンプルにし、FFTを通したもの。
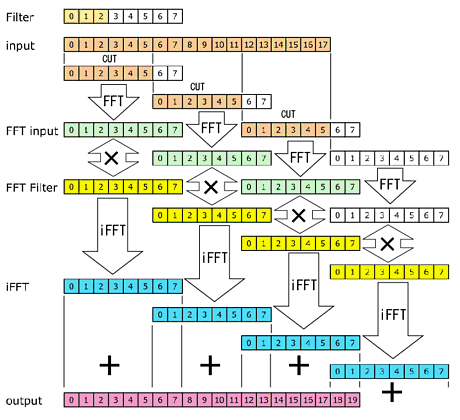
Wikiにも原理の解説があったのでリンクしておきます。 http://ja.wikipedia.org/wiki/重畳加算法
P=L+M-1
この式は、あるサンプル数の入力信号と、あるサンプル数のフィルタ信号を畳み込むと、必要なサンプル数が増えるので、そのサンプル数を求める式。
P: 出力の長さ(FFTに入れるサンプル数)
L: FFTにかける入力サンプル数(全体の長さではない)
M: フィルタのサンプル数
ここに分かっている数値を入れて、Lを導いてみる。
8=L+3-1
L=6
LはMよりも大きいという条件にしたが、自己流なので本来どのように計算するかは不明。いつものように少ない資料や式から、こじつけでプログラム化してます。今回は3サンプルなので、FFTは2^nなので、8サンプルもしくは、16サンプルが使えそうだ。ただ16サンプルだと無駄が多いので、この場合8サンプルが適当となる。ここまで決まったら、入力信号のサンプル数を計算する。
フィルタのサンプル数MとFFT用サンプル数Pが決まれば、上記計算式で入力信号は6サンプルで切ればよいことが分かる。FFTには8サンプル分入れて計算するので、残りの2サンプルには0を入れてしまう。同じようにフィルタもサンプル数が3なので、残りの5サンプルには0を入れてしまう。
コンパイルして実行すると以下のような結果が表示される。2サンプル遅れているのが確認できる。
sound programming 目次はこちら
下図は、この記事のプログラムを図式化したもの。数字はサンプル数でプログラムと対応している。色の付いていないマスにはデータがないので値0を入れている。FilterのFFT処理はレイアウト上、矢印が引けなかったので、唐突に黄色く8サンプルで出てくるけど、上段のFilterの色がある3サンプルに値0の5サンプルを加えて8サンプルにし、FFTを通したもの。

Wikiにも原理の解説があったのでリンクしておきます。 http://ja.wikipedia.org/wiki/重畳加算法
入力信号のサンプル数の決定方法
下のプログラムではフィルタのサンプル数を元に計算している。P=L+M-1
この式は、あるサンプル数の入力信号と、あるサンプル数のフィルタ信号を畳み込むと、必要なサンプル数が増えるので、そのサンプル数を求める式。
P: 出力の長さ(FFTに入れるサンプル数)
L: FFTにかける入力サンプル数(全体の長さではない)
M: フィルタのサンプル数
ここに分かっている数値を入れて、Lを導いてみる。
8=L+3-1
L=6
LはMよりも大きいという条件にしたが、自己流なので本来どのように計算するかは不明。いつものように少ない資料や式から、こじつけでプログラム化してます。今回は3サンプルなので、FFTは2^nなので、8サンプルもしくは、16サンプルが使えそうだ。ただ16サンプルだと無駄が多いので、この場合8サンプルが適当となる。ここまで決まったら、入力信号のサンプル数を計算する。
フィルタのサンプル数MとFFT用サンプル数Pが決まれば、上記計算式で入力信号は6サンプルで切ればよいことが分かる。FFTには8サンプル分入れて計算するので、残りの2サンプルには0を入れてしまう。同じようにフィルタもサンプル数が3なので、残りの5サンプルには0を入れてしまう。
窓関数について
入力信号から周波数スペクトルを計算するときは窓関数は必須だが、今回のoverlap-add methodでは、入力信号には窓関数などを掛ける必要はなく、そのままダイレクトに計算する。フィルタは係数を求めるときには窓関数は必要だが、今回はすでにそのような処理が終わったフィルタを入れていることを前提としている。FFT overlap-add method 実験用ソースコード
やや見にくいソースになってしまった。フィルタのFFTは1回でよいので、はじめに計算している。入力信号は分割してからFFT、畳み込み、iFFTで出力まで行って出力用配列に入れている。下記のサンプルだと 18/6+1=4 で4回繰り返している。このサンプル数からすれば3回でよいのだけど、中途半端なサンプル数だと計算がこぼれてしまうので、1つ多めにしている。また入力信号やフィルタの数を多少変えても実行するようにしているけど、条件が合わないと、でたらめな出力をすると思われる。こんな感じのプログラムを実用的に改造することで、実際の音声ファイルを、そこそこ高速にFIR処理できるようになる。 |
i=1 P=2 L=0 M=3 i=2 P=4 L=2 M=3 i=3 P=8 L=6 M=3 Filter FFT N: FFT Real FFT Imaginary FFT Power 0: 1.00000000000 0.00000000000 1.00000000000 1: 0.00000000000 -1.00000000000 1.00000000000 2: -1.00000000000 0.00000000000 1.00000000000 3: -0.00000000000 1.00000000000 1.00000000000 4: 1.00000000000 0.00000000000 1.00000000000 5: 0.00000000000 -1.00000000000 1.00000000000 6: -1.00000000000 0.00000000000 1.00000000000 7: -0.00000000000 1.00000000000 1.00000000000 input:0 sample P= 8tap L=6tap for FFT 0: 0.100000 0.000000 1: 0.200000 0.000000 2: 0.300000 0.000000 3: 0.400000 0.000000 4: 0.500000 0.000000 5: 0.600000 0.000000 6: 0.000000 0.000000 7: 0.000000 0.000000 FFT0 FFT input r FFT imput i 0: 2.10000000000 0.00000000000 1: -0.96568542495 -0.30000000000 2: 0.30000000000 -0.40000000000 3: 0.16568542495 0.30000000000 4: -0.30000000000 0.00000000000 5: 0.16568542495 -0.30000000000 6: 0.30000000000 0.40000000000 7: -0.96568542495 0.30000000000 comv:0 convolution r convolution i 0: 2.10000000000 0.00000000000 1: -0.30000000000 0.96568542495 2: -0.30000000000 0.40000000000 3: -0.30000000000 0.16568542495 4: -0.30000000000 0.00000000000 5: -0.30000000000 -0.16568542495 6: -0.30000000000 -0.40000000000 7: -0.30000000000 -0.96568542495 yi:0: iFFT Real iFFT Imaginary 0: -0.00000000000 0.00000000000 1: 0.00000000000 0.00000000000 2: 0.10000000000 0.00000000000 3: 0.20000000000 0.00000000000 4: 0.30000000000 0.00000000000 5: 0.40000000000 -0.00000000000 6: 0.50000000000 -0.00000000000 7: 0.60000000000 -0.00000000000 input:1 sample P= 8tap L=6tap for FFT 0: 0.700000 0.000000 1: 0.800000 0.000000 2: 0.900000 0.000000 3: 1.000000 0.000000 4: 0.900000 0.000000 5: 0.800000 0.000000 6: 0.000000 0.000000 7: 0.000000 0.000000 FFT1 FFT input r FFT imput i 0: 5.10000000000 0.00000000000 1: -0.90710678119 -1.60710678119 2: 0.70000000000 -0.60000000000 3: 0.50710678119 0.19289321881 4: -0.10000000000 0.00000000000 5: 0.50710678119 -0.19289321881 6: 0.70000000000 0.60000000000 7: -0.90710678119 1.60710678119 comv:1 convolution r convolution i 0: 5.10000000000 0.00000000000 1: -1.60710678119 0.90710678119 2: -0.70000000000 0.60000000000 3: -0.19289321881 0.50710678119 4: -0.10000000000 0.00000000000 5: -0.19289321881 -0.50710678119 6: -0.70000000000 -0.60000000000 7: -1.60710678119 -0.90710678119 yi:1: iFFT Real iFFT Imaginary 0: -0.00000000000 0.00000000000 1: -0.00000000000 0.00000000000 2: 0.70000000000 -0.00000000000 3: 0.80000000000 0.00000000000 4: 0.90000000000 -0.00000000000 5: 1.00000000000 -0.00000000000 6: 0.90000000000 0.00000000000 7: 0.80000000000 0.00000000000 input:2 sample P= 8tap L=6tap for FFT 0: 0.700000 0.000000 1: 0.600000 0.000000 2: 0.500000 0.000000 3: 0.400000 0.000000 4: 0.300000 0.000000 5: 0.200000 0.000000 6: 0.000000 0.000000 7: 0.000000 0.000000 FFT2 FFT input r FFT imput i 0: 2.70000000000 0.00000000000 1: 0.40000000000 -1.06568542495 2: 0.50000000000 -0.40000000000 3: 0.40000000000 -0.06568542495 4: 0.30000000000 0.00000000000 5: 0.40000000000 0.06568542495 6: 0.50000000000 0.40000000000 7: 0.40000000000 1.06568542495 comv:2 convolution r convolution i 0: 2.70000000000 0.00000000000 1: -1.06568542495 -0.40000000000 2: -0.50000000000 0.40000000000 3: 0.06568542495 0.40000000000 4: 0.30000000000 0.00000000000 5: 0.06568542495 -0.40000000000 6: -0.50000000000 -0.40000000000 7: -1.06568542495 0.40000000000 yi:2: iFFT Real iFFT Imaginary 0: 0.00000000000 0.00000000000 1: 0.00000000000 0.00000000000 2: 0.70000000000 0.00000000000 3: 0.60000000000 0.00000000000 4: 0.50000000000 -0.00000000000 5: 0.40000000000 -0.00000000000 6: 0.30000000000 -0.00000000000 7: 0.20000000000 0.00000000000 input:3 sample P= 8tap L=6tap for FFT 0: 0.000000 0.000000 1: 0.000000 0.000000 2: 0.000000 0.000000 3: 0.000000 0.000000 4: 0.000000 0.000000 5: 0.000000 0.000000 6: 0.000000 0.000000 7: 0.000000 0.000000 FFT3 FFT input r FFT imput i 0: 0.00000000000 0.00000000000 1: 0.00000000000 0.00000000000 2: 0.00000000000 0.00000000000 3: 0.00000000000 0.00000000000 4: 0.00000000000 0.00000000000 5: 0.00000000000 0.00000000000 6: 0.00000000000 0.00000000000 7: 0.00000000000 0.00000000000 comv:3 convolution r convolution i 0: 0.00000000000 0.00000000000 1: 0.00000000000 0.00000000000 2: 0.00000000000 0.00000000000 3: 0.00000000000 0.00000000000 4: 0.00000000000 0.00000000000 5: 0.00000000000 0.00000000000 6: 0.00000000000 0.00000000000 7: 0.00000000000 0.00000000000 yi:3: iFFT Real iFFT Imaginary 0: 0.00000000000 0.00000000000 1: 0.00000000000 0.00000000000 2: 0.00000000000 0.00000000000 3: 0.00000000000 0.00000000000 4: 0.00000000000 0.00000000000 5: 0.00000000000 0.00000000000 6: 0.00000000000 0.00000000000 7: 0.00000000000 0.00000000000 output 0: -0.00000000000 output 1: 0.00000000000 output 2: 0.10000000000 output 3: 0.20000000000 output 4: 0.30000000000 output 5: 0.40000000000 output 6: 0.50000000000 output 7: 0.60000000000 output 8: 0.70000000000 output 9: 0.80000000000 output 10: 0.90000000000 output 11: 1.00000000000 output 12: 0.90000000000 output 13: 0.80000000000 output 14: 0.70000000000 output 15: 0.60000000000 output 16: 0.50000000000 output 17: 0.40000000000 output 18: 0.30000000000 output 19: 0.20000000000 |
sound programming 目次はこちら
